几何·消点法

以下内容是笔者在阅读作者中璋的《写给青少年的数学故事（下）：几何妙想》一书时的读书笔记。

消点法，是一种将线段间的关系与三角形面积间的关系相互转化的方法。简单地说，就是线段的比例与三角形面积的比例之间的转化。

消点法的基础是面积法，而面积法基于有关三角形面积的两个定理：共高定理和共边定理。

共高&共边定理

共高定理：如果两个三角形高相同，则面积比等于底之比。

$$\frac {S_{△PAM}} {S_{△PBM}} = \frac {AM} {BM}$$

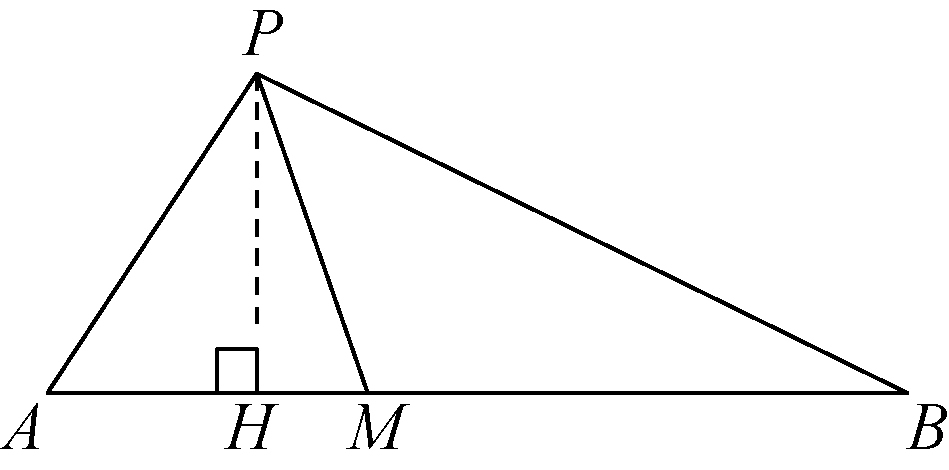
【关于证明】通过三角形面积公式，易证。

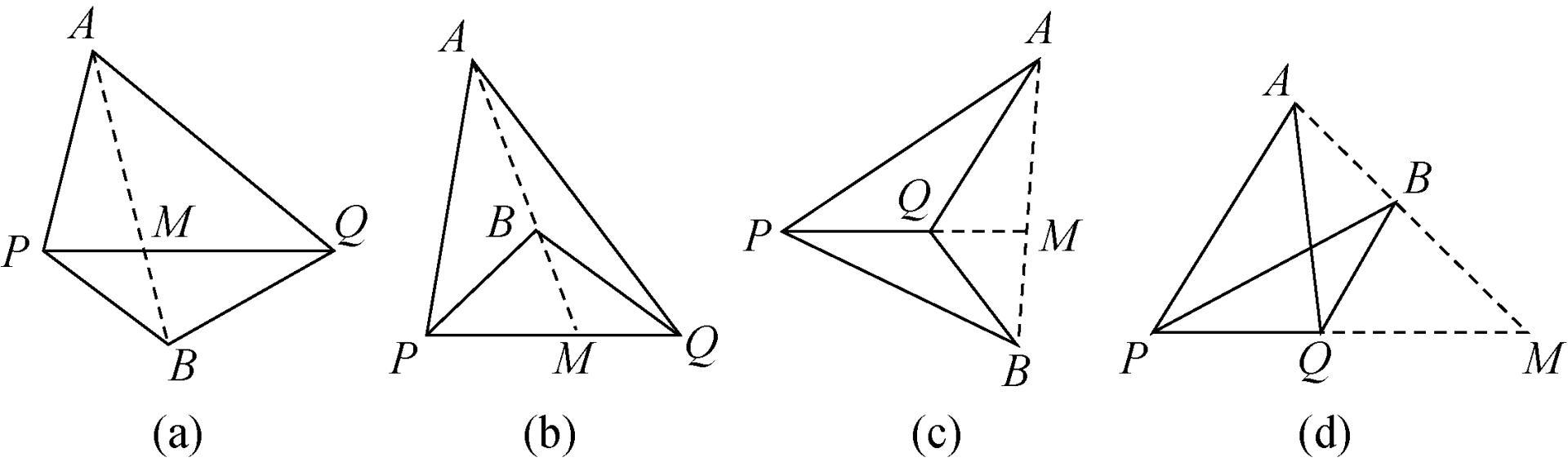
共边定理：如果两个三角形底相同：

1. 面积比等于高之比；
2. 另一顶点连线 AB 和底（或其延长线）交于 M，则面积比等于 AM : BM。

$$\frac {S_{△QPA}} {S_{△QPB}} = \frac {AM} {BM}$$

\

【关于证明】

1. 与共高类似，用三角形面积公式即可证。
2. 设两三角形的高与共边的交点分别为 A’ 和 B’，则通过证明 $S{△AA’M} ∽ S{△BB’M}$ 即可将高之比转化为两者斜边的比。

例题

已知：在 $△ABC$ 中，AD : DC = 1 : 2，BE : EC = 3 : 2。求 BF : DF。

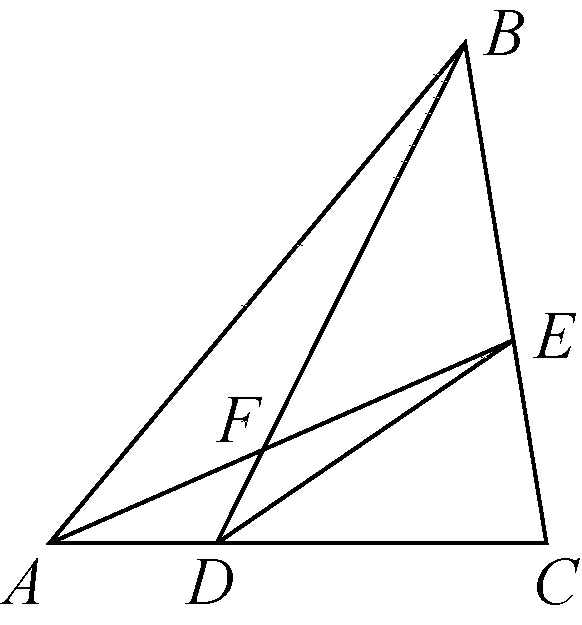
解：

要求 BF : DF，根据共边（AE）定理可得：

$$\frac {BF} {DF} = \frac {S_{△AEB}} {S_{△AED}} \qquad (1)$$

根据 $S_{△AEB}$ 与已知比例 BE : EC，用共边（AE）定理得：

$$\frac {S_{△AEB}} {S_{△AEC}} = \frac {BE} {EC} \qquad (2)$$

为了把式(2)代入式(1) ，则还需要通过共高定理得：

$$\frac {S_{△AEC}} {S_{△AED}} = \frac {AC} {AD} \qquad (3)$$

至此可将式(1)变形并将式(2)、(3)代入得：

$$\begin{flalign*} \frac {BF} {DF} & = \frac {S_{△AEB}} {S_{△AED}} = \frac {S_{△AEB}} {S_{△AEC}} \cdot \frac {S_{△AEC}} {S_{△AED}} \\ & = \frac {BE} {EC} \cdot \frac {AC} {AD} & & \\ & = \frac 3 2 \cdot \frac 3 2 & & \\ & = \frac 9 4 \end{flalign*}$$

【解说】

根据消点法，可以对图形中的点进行分组， 分组的依据是点的约束性及其约束层级。以上例题来说明，可将图中的点分为三组：

• 组1：A、B、C，称为“自由点”，无约束
• 组2：D、E，称为“约束点”，根据已知中的比例要求，受 A、B、C 约束
• 组3：F，也是“约束点”，但更低一级，受 D、E 的约束

消点法的原理是，约束点 D、E 由自由点 A、B、C 约束，因此可用 A、B、C 间数量关系表示。低级的约束点 F，可用 A、B、C 和 D、E 数量关系表示。

因此，约束点相关的比例关系，最终可以转化为自由点相关的比例关系。消去约束点，即为消点。