（科赫）雪花曲线及反雪花曲线的周长和面积推导

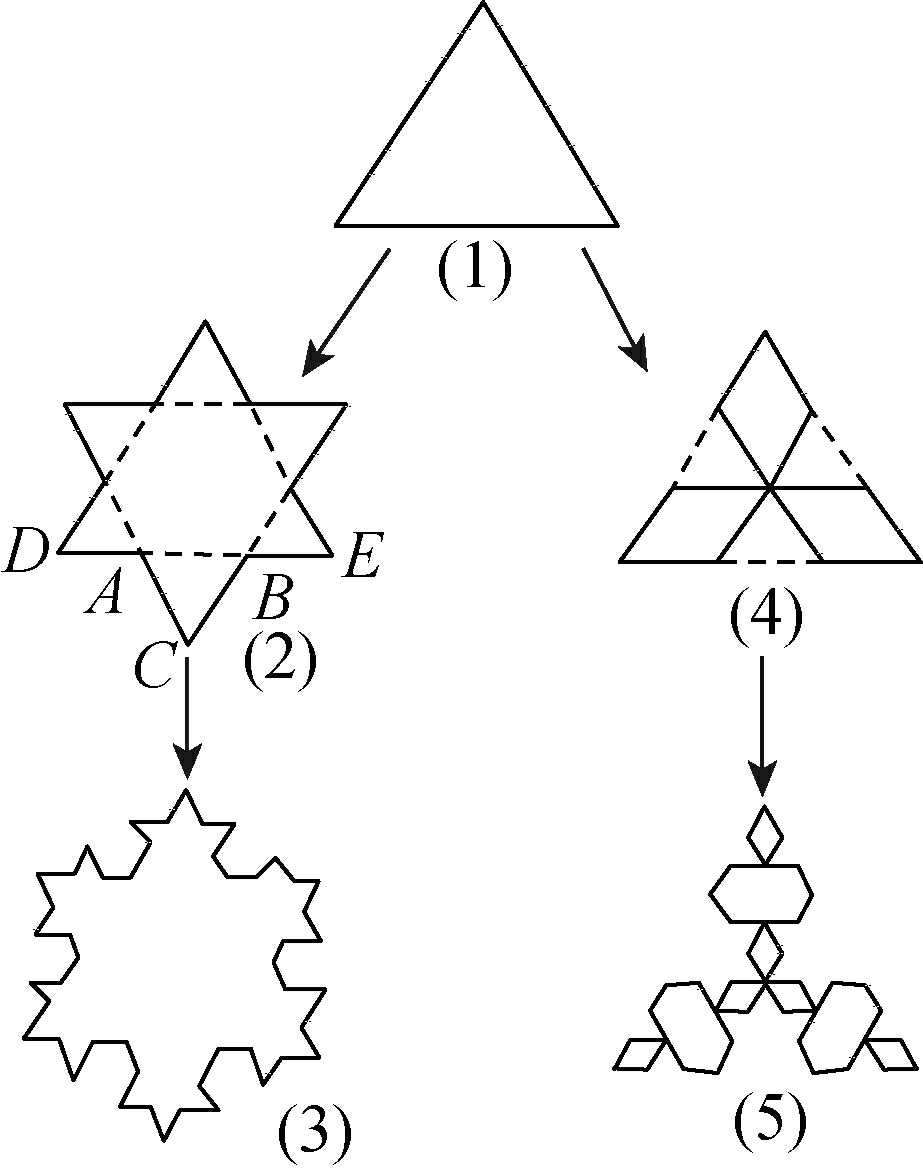
雪花曲线

图中(1)→(2)→(3)是雪花曲线的演化……

雪花曲线周长极限是多少？

每次演化，1/3 条边就变换成了两个 1/3 条边的角。因此，第n个雪花图形的周长是：

$$\begin{flalign*} & L_n = \frac {4} {3} L_{n-1} = (\frac 4 3)^{n-1} L_1 \\ & \\ \end{flalign*}$$

它的极限是：

$$\lim_{n \to \infty} L_n = {\infty}$$

雪花曲线面积极限是多少？

$$\begin{array}{c|rrr} \hline & \text{边长} & \text{个数} & \text{面积} \\ \hline S_0 & L_0 & 1 & S_0 \\ S_1 & (\frac 1 3)^1 L_0 & 3 & (\frac 1 9)^1S_0 \\ S_2 & (\frac 1 3)^2L_0 & 3 × 4 & (\frac 1 9)^2S_0 \\ \vdots & \vdots & \vdots & \vdots \\ S_n & (\frac 1 3)^nL_0 & 3 × 4^{n-1} & (\frac 1 9)^nS_0 \end{array}$$

上表中，各列分别指的是每次演化，凸出的三角形的边长、个数和单个的面积。

因此，累加每行个数×面积即为 $S_n$ 的面积：

$$S_n = S_0[1 + 3 × \frac 1 9 + 3 × 4 × (\frac 1 9)^2 + \cdots + 3 × 4^{n-1} × (\frac 1 9)^n]$$

整理下 $3 × \frac 1 9, \cdots, 3 × 4^{n-1} × (\frac 1 9)^n$ 则会发现这是个通项为 $\frac 1 3 ×(\frac 4 9)^{n-1}$ 等比数列，根据等比数列前n项各公式可得：

$$\begin{align} & \frac 1 3 + \frac 1 3 × \frac 4 9 + \cdots + \frac 1 3 ×(\frac 4 9)^{n-1} \\ = & \frac 1 3 \left[ \frac {1-(\frac 4 9)^{n-1}} {1-{\frac 4 9}} \right] \\ = & \frac 3 5 × \left[ 1-(\frac 4 9)^{n-1} \right] \end{align}$$

代入 $S_n$ 等式右侧可得：

$$S_n = S_0\left\{ 1 + \frac 3 5 \left[ 1-(\frac 4 9)^{n-1} \right] \right\}$$

求极限可得：

$$\lim_{n \to \infty} S_n = \frac 8 5 S_0$$

因此，雪花曲线的极限面积是初始面积的 $\frac 8 5$。

反雪花曲线

图中(1)→(4)→(5)是反雪花曲线的演化……

反雪花曲线周长极限是多少？

虽然，反雪花曲线是“向内”演化的，但是它的周长增长情况与雪花曲线是完全相同的。也就是说，周长的极限也是 $\infty$。

【反直觉】
是的，这是反直觉的。一个封闭范围内的图形，周长是无限的。

反雪花曲线面积极限是多少？

反雪花曲线与雪花曲线的面积情况正好相反，不是增加面积，反而是减少相同的面积，因此：

$$S_n = S_0\left\{ 1 - \frac 3 5 \left[ 1-(\frac 4 9)^{n-1} \right] \right\}$$

所以，反雪花曲线面积的极限是初始面积的 $\frac 2 5$。

$$\lim_{n \to \infty} S_n = \frac 2 5 S_0$$